重回帰分析　 　一つの変数を複数の変数で説明するモデルの適切さや，説明力などについて分析する手法です。説明される変数を従属変数，説明する変数を独立変数とよびますね。イメージとしては，偏相関係数の発展と考えてもよいでしょう。 　ですので，重回帰分析をする時には，事前に全変数間の相関係数，偏相関係数を眺めてみて，考えているモデルは適当なのかどうかについて少し考えておくとよいと思います。もちろん，変数間の関係は直線的関係が仮定できないとダメです。 　さて，手順ですが以下のように開きます。 　　分析 　　　　→　回帰 　　　　　→　線型 　そうすると，「線型回帰」というダイアログボックスが表示されます。ここで説明される変数を「従属変数」，説明する変数を「独立変数」のボックスに移動させてやればよいわけです。最も単純な指定はこれで終わりです。 　もう少し各種統計量を計算したい時は，右の「統計」を活用すればよいでしょう。新しく開く「線型回帰：統計」のダイアログボックスで「記述統計量」にチェックすると，各変数の平均などや相関係数を出力してくれます。「部分/偏相関」をチェックすると，ゼロ次相関（通常の相関係数），偏相関係数，部分相関係数を計算してくれます。また「共線性の診断」にチェックをしておくと，VIFという指標を計算してくれます（一般的には，これが10を越えると多重共線性がうたがわれます）。 　なお出力に関しては，当然ですが，最初に回帰式の有意性についてみます。「モデル要約」という表に，「R（重相関係数）」，「R2乗（重決定係数）」，「調整済みR2乗（自由度調整済みの重決定係数）」が示され，その下の「分散分析」という表にこれの有意性を検定した分散分析の結果が出力されます。この分散分析の結果が有意であれることを確認した上で，各変数間の標準偏回帰整数を見るということになります。 　偏回帰係数については，「係数」という表に出力されます。「標準化係数」「ベータ」という欄の数値が，標準偏回帰係数（β）になります。その横にt値と有意確率が載っていますが，これが係数に対する検定結果です。ちなみに「非標準化係数」の「B」は偏回帰係数で，予測式を作る時などに役立つものです。 ●独立変数間の相関が高い場合の例 　独立変数間の相関が高い場合，重回帰分析の結果，相関係数，偏相関係数がどのようになっているのかを例示してみます。 　モデルとしては，a1が従属変数，b1，b2，b3を独立変数と考えていました。このモデルで重回帰分析を行ったところ，「調整済みR2乗」=.405で有意なものでした。そこで標準偏回帰係数を見てみると，以下のようだったとします。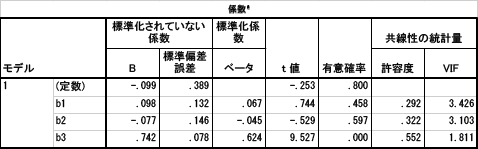 　つまり，有意な関連性を持つ変数はb3のみであるという結果になります。しかし，b1やb2は，a1と相関を持たないような変数ではありません。「記述統計量」にチェックを入れて項目間の相関係数を求めると，以下のようにb1やb2もa1と中程度の相関関係にあるのです。しかし，重回帰分析の結果では，これらは関連が認められないという結果になったわけです。このような結果になった背景には，独立変数間の関連の強さが影響していると考えられます。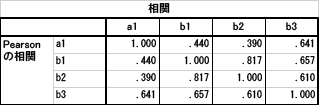 　そこで，「部分/偏相関」をチェックして，a1とb1，b2，b3の間の偏相関係数を計算させてみました。その結果が下の表です。右側にある「相関」の「ゼロ次」という部分が通常の相関係数になります。上の表と同じ値であることを確認してください。その隣の「偏」という部分が偏相関係数です。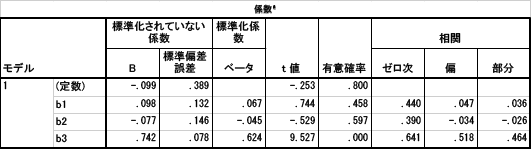 　また，b1，b2の間の偏相関係数（a1，b3を統制），b1，b3の間の偏相関係数（a1，b2を統制），b2，b3の間の偏相関係数（a1，b1を統制）を求めてみました。すると順に，.698**，.272**，.161(ns)という結果でした。 　これらの偏相関係数を中心とした結果を眺めてみると，a1とb3，b1とb2が密接な関係にあり，また，b3はb2とも関連していることがわかります。すなわち，下図の上のモデルのような変数間の関係ではなく，下のモデルのような関係ではないかと推測できるのです。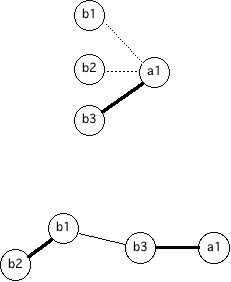 　もし，論理的に下のモデルよりも上のモデルが妥当であるならば，独立変数間にある比較的強い相関が重回帰分析に影響していると考えられます。すると今回の重回帰分析の結果から，b3のみが強く関連していると主張することは適当ではないでしょう。データの特徴と方法が適切に対応していないのですから。こうなると，方法を再考するしかありません。共分散構造分析が代替案になります。 　しかし，偏相関係数から考えられた下のモデルも論理的に妥当と考えられるならば，上のモデルを破棄することも適当といえます。そして下のようなモデルを仮定してさらに考えていくわけです。 　このように独立変数間の相関が高い場合は，いろいろと他にやること，考えることが出てきます。重回帰分析の結果だけで満足しない方が生産的です。 ***********シンタックス 　重回帰分析は，REGRESSION を使います。最も単純な指定をダイアログボックスで指定してシンタックスに書き出すと，以下のようになります。 REGRESSION 　/MISSING_LISTWISE 　/STATISTICS_COEFF_OUTS_R_ANOVA 　/CRITERIA=PIN(.05)_POUT(.10) 　/NOORIGIN 　/DEPENDENT_a1 　/METHOD=ENTER_b1_b2_b3. となります。半角アケの部分が見えにくいので，_（アンダーバー）にしてあります。省略可能なものもいくつか含まれていますが… ●さらに，記述統計をチェックすると…（/DESCRIPTIVES の部分が加わります） REGRESSION 　/DESCRIPTIVES MEAN STDDEV CORR SIG N 　/MISSING LISTWISE 　/STATISTICS COEFF OUTS R ANOVA 　/CRITERIA=PIN(.05) POUT(.10) 　/NOORIGIN 　/DEPENDENT a1 　/METHOD=ENTER b1 b2 b3. ●ステップワイズ（投入方法は/METHOD で指定します） REGRESSION 　/MISSING LISTWISE 　/STATISTICS COEFF OUTS R ANOVA 　/CRITERIA=PIN(.05) POUT(.10) 　/NOORIGIN 　/DEPENDENT a1 　/METHOD=STEPWISE b1 b2 b3.